Quantum DeepONet: Neural operators accelerated by quantum computing
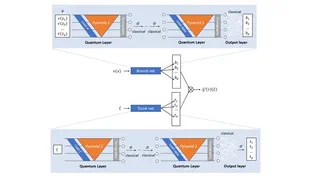 Architecture of quantum DeepONet
Architecture of quantum DeepONetAbstract
In the realm of computational science and engineering, constructing models that reflect real-world phenomena requires solving partial differential equations (PDEs) with different conditions. Recent advancements in neural operators, such as deep operator network (DeepONet), which learn mappings between infinite-dimensional function spaces, promise efficient computation of PDE solutions for a new condition in a single forward pass. However, classical DeepONet entails quadratic complexity concerning input dimensions during evaluation. Given the progress in quantum algorithms and hardware, here we propose to utilize quantum computing to accelerate DeepONet evaluations, yielding complexity that is linear in input dimensions. Our proposed quantum DeepONet integrates unary encoding and orthogonal quantum layers. We benchmark our quantum DeepONet using a variety of PDEs, including the antiderivative operator, advection equation, and Burgers’ equation. We demonstrate the method’s efficacy in both ideal and noisy conditions. Furthermore, we show that our quantum DeepONet can also be informed by physics, minimizing its reliance on extensive data collection. Quantum DeepONet will be particularly advantageous in applications in outer loop problems which require to explore parameter space and solving the corresponding PDEs, such as uncertainty quantification and optimal experimental design.
Type